समय और कार्य से संबंधित प्रश्न प्रतियोगिता परीक्षाओं में पूछे जाते हैं। इस टाॅपिक के बारे में हमलोग पूर्व कक्षाओं में भी पढ़ चुके हैं। पूर्व कक्षाओं में पढ़ने के बावजूद इससे संबंधित प्रश्नों को प्रतियोगिता परीक्षाओं में हल करने के लिए हमें और अधिक जानकारी की आवश्यकता होती है। इन प्रश्नों को हल करने के लिए परीक्षाओं में एक समय-सीमा दी गई होती है। यहाँ हमें कुछ ऐसे तरीके बतायें गये हैं जिससे दी गई समय-सीमा के अंदर हम प्रश्नों को हल कर सकेंगे।
प्रश्नों को हल करने की संक्षिप्त विधि
यदि कोई आदमी किसी कार्य को ‘m’ दिन में पूरा करता हो तो वह एक दिन में उस कार्य का 1/m भाग ही पूरा कर सकता है।
उदाहरण 1. राम किसी कार्य को 15 दिन में करता है तो 2 दिन में वह कितना भाग काम करता है?
हल: यहाँ दिया हुआ है, राम 15 दिन में एक काम करता है।
∴ 2 दिनों में वह ![]() × 2 =
× 2 = ![]() भाग काम करता है।
भाग काम करता है।
- यदि किसी कार्य को पूरा करने में लगे व्यक्तियों की संख्या एक निश्चित अनुपात में बढ़ायी (या घटायी) जाए तो उसी कार्य को पूरा करने में आवश्यक समय उसी अनुपात में बढ़ता या घटता है।
- यदि किसी व्यक्ति A की किसी अन्य व्यक्ति B से कार्य करने की क्षमता दुगुनी हो तो किसी कार्य को समाप्त करने में A, B से आधा समय लेगा।
उदाहरण 2. राम की कार्य करने की क्षमता श्याम से दुगुनी है। यदि श्याम किसी कार्य को 30 दिनों में पूरा करता है तो बताइये राम उस कार्य को कितने दिनों में पूरा करेगा?
हल: चूँकि राम के कार्य करने की क्षमता श्याम से दुगुनी है,
इसलिए वह उस काम को ![]() दिनों में पूरा करेगा।
दिनों में पूरा करेगा।
समय और कार्य हमेशा एक-दूसरे के समानुपाती होते हैं।
यदि A और B अकेले किसी कार्य को क्रमशः X और Y दिनों में पूरा करते हैं, तो वे दोनों साथ मिलकर उसी कार्य को ![]() दिनों में पूरा करेंगे।
दिनों में पूरा करेंगे।
प्रमाण: A का 1 दिन का कार्य = 1/x
B का 1 दिन का कार्य = 1/y
इसलिए (A + B) का 1 दिन का कार्य
= कुल कार्य का ![]()
माना कुल कार्य W है।
अब, 1 दिन में W का ![]() भाग कार्य पूरा होता है।
भाग कार्य पूरा होता है।
∴ W (कुल कार्य) पूरा होगा 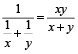 दिनों में।
दिनों में।
उदाहरण 3. श्याम एक कार्य को 30 दिनों में पूरा करता है। राम उसी कार्य को 15 दिनों में पूरा करता है तो वे दोनों मिलकर उस कार्य को कितने दिनों में पूरा करेंगे?
हल: सूत्र के अनुसार, अभीष्ट दिन
= ![]() दिन
दिन
यदि A, B और C किसी कार्य को अकेले क्रमशः X, Y और Z दिनों में पूरा करते हैं तो वे तीनों मिलकर उसी काम को ![]() दिनों में पूरा करेंगे।
दिनों में पूरा करेंगे।
उदाहरण 4. श्याम एक कार्य को 30 दिनों में पूरा करता है, राम उसी कार्य को 15 दिनों में पूरा करता है और भुवन उस कार्य को 10 दिनों में पूरा करता है। वे तीनों मिलकर इस कार्य को कितने दिनों में पूरा करेंगे?
हल: सूत्र के अनुसार, अभीष्ट दिन
![]()
= ![]() दिन
दिन
यदि A किसी कार्य को X दिनों में, B, Y दिनों में और A, B और C तीनों मिलकर उसी कार्य को S दिनों में पूरा करते हैं तोः
(i) C अकेले उस कार्य को ![]() दिनों में पूरा करेगा।
दिनों में पूरा करेगा।
(ii) B + C उस कार्य को ![]() दिनों में पूरा करेगा।
दिनों में पूरा करेगा।
(iii) A + C उस कार्य को ![]() दिनों में पूरा करेगा।
दिनों में पूरा करेगा।
उदाहरण 5. A और B किसी कार्य को 6 दिनों में पूरा कर सकते हैं और A अकेले उस कार्य को 9 दिनों में पूरा कर सकता है। B अकेले उस कार्य को कितने दिनों में पूरा कर सकता है?
हल: (A + B) का 1 दिन का कार्य = पूरे कार्य का 1/6 भाग
A का 1 दिन का कार्य = पूरे कार्य का 1/9 भाग
∴ B का 1 दिन का कार्य
= ![]() = पूरे कार्य का 1/18 भाग
= पूरे कार्य का 1/18 भाग
∴ B अकेले उस कार्य को 18 दिनों में कर सकता है।
उदाहरण 6. A और B अकेले किसी कार्य को क्रमशः 6 दिनों और 12 दिनों में कर सकता है। दोनों एक साथ कार्य करना प्रारंभ करते हैं लेकिन कार्य पूरा होने से 3 दिन पहले A कार्य करना छोड़ देता है। कितने दिनों में कार्य पूरा होगा?
- 6 दिनों में
- 4 दिनों में
- 5 दिनों में
- 7 दिनों में
हल: (1) माना कार्य X दिन में पूरा होगा।
A द्वारा (X – 3) दिनों में किया गया कार्य + B द्वारा X दिनों में किया गया कार्य = 1
अर्थात् ![]()
⇒ ![]() = 1
= 1
⇒ x = 6 दिन
उदाहरण 7. A के कार्य करने की क्षमता B से आधी है। दोनों मिलकर किसी कार्य को 14 दिनों में पूरा करते हैं। B अकेले उस कार्य को कितने दिनों में पूरा करेगा?
- 20 दिनों में
- 21 दिनों में
- 22 दिनों में
- इनमें से कोई नहीं
हल: (2) माना B, X दिनों में कार्य पूरा कर सकता है तो A उस कार्य को 2x दिनों में करेगा।
तब, ![]() (दिया हुआ है)
(दिया हुआ है)
⇒ ![]() = 21 दिन
= 21 दिन
उदाहरण 8. 10 पुरूष किसी कार्य को 10 दिनों में पूरा करते हैं जबकि 12 महिला भी उसी कार्य को 10 दिनों में पूरा करती हैं। यदि 15 पुरूष और 6 महिलाएँ कार्य को पूरा करने की जिम्मेदारी लेते हैं तो वे कितने दिनों में कार्य को पूरा करेंगे?
- 7 दिनों में
- 5 दिनों
- 4 दिनों में
- 6 दिनों
हल: (2) यह स्पष्ट है कि
10 पुरूष = 12 महिलाएँ या 5 पुरूष = 6 महिलाएँ
⇒ 15 पुरूष + 6 महिलाएँ = (18 + 6) अर्थात् 24 महिलाएँ
अब, 12 महिलाएँ कार्य को 10 दिनों में पूरा करती हैं
∴24 महिलाएँ 5 दिनों में कार्य पूरा करेंगी।
सूत्र द्वारा:
अभीष्ट समय
= ![]() दिन
दिन
यदि ‘M₁’ व्यक्ति, ‘W₁’ कार्य को ‘D₁’ दिनों में करता हो और ‘M₂’ व्यक्ति ‘W₂’ कार्य को ‘D₂’ दिनों में करता हो, तो
M₁ D₁ W₂ = M₂ D₂ W₁
यदि T₁ T₂ दो समूहों की कार्य अवधि हो, तो
M₁ D₁ W₂ T₁ = M₂ D₂ W₁ T₂
इसी तरह, M₁ D₁ W₂ T₁ E₁ = M₂ D₂ W₁ T₂ E₂
जहाँ E₁ और E₂ दो समूहों के कार्य करने की क्षमता है।
यदि किसी कार्य को पूरा करने में लगे व्यक्तियों की संख्या a:b के अनुपात में परिवर्तित हो, तो कार्य को पूरा करने में आवश्यक समय का अनुपात b:a होगा जबकि दिए गए समय में प्रत्येक के कार्य करने की क्षमता एक समान है।
A के कार्य करने की क्षमता B से k गुणी हो और A, B से X दिन कम समय में कार्य को पूरा करता हो, तो A और B द्वारा एक साथ कार्य को पूरा करने में लगा आवश्यक समय ![]() दिन होगा।
दिन होगा।
यदि A की क्षमता B से n गुणी हो अर्थात् A के कार्य करने की क्षमता B से n गुणी हो, तो A उस कार्य को पूरा करने में B द्वारा लिये गए समय का 1/n समय लेगा।
उदाहरण 9. 6 घंटे प्रतिदिन कार्य करके 6 दिन में 5 व्यक्ति, 10 खिलौने बनाते हैं। 8 घंटे प्रतिदिन कार्य करके 12 व्यक्ति, 16 खिलौने कितने दिनों में बनाएँगे?
हल: हम जानते हैं कि,M₁ D₁ T₁ W₂ = M₂ D₂ T₂ W₁
यहाँ 5 × 6 × 6 × 16 = 12 × D₂ × 8 × 10
∴ ![]() = 3 दिन
= 3 दिन
