Finish Test
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
- अति महत्वपूर्ण बहु वैकल्पिक प्रश्न
- ऑनलाइन ज्यामिति एक्सरसाइज, उत्तर और हल के साथ
- सभी प्रत्योगिता परीक्षाओं के लिए उपयोगी
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
- Question 1 of 20
1. Question
किसी बहुभुज के अंतःकोणों का योग 1620° है। बहुभुज के भुजाओं की संख्या हैः
Hint
The sum of the interior angles of a polygon of n sides is given by the expression (2n – 4) π/2
⇒
⇒ 2n = 22
⇒ n = 11
Thus the no. of sides of the polygon are 11.
- Question 2 of 20
2. Question
एक चक्रीय चतुर्भुज जिसकी आसन्न भुजाएँ असमान हैं, अवश्य ही होगीः
Hint
It is a rectangle.
(In a cyclic parallelogram each angle is equal to 90°. So, it is definitely either a square or a rectangle. Since the given cyclic parallelogram has unequal adjacent sides, it is a square.)
- Question 3 of 20
3. Question
यदि किसी त्रिभुज के कोणों का अनुपात 5:3:2 है, तो त्रिभुज होगाः
Hint
Let the angles of the triangle be 5x, 3x and 2x.
Now, 5x + 3x + 2x = 180°
⇒ 10x = 180
⇒ x = 18
⇒ Angles are 36, 54 and 90°
Given ∆ is right angled.
- Question 4 of 20
4. Question
यदि किसी समचतुर्भुज का एक विकर्ण इसकी भुुजा के बराबर है, तो समचतुर्भुज के विकर्णों का अनुपात है।
Hint
Let the diagonals of the rhombus be x and y and the its sides be x
Now,
⇒
⇒ 3x² = y²
⇒
⇒ y : x
- Question 5 of 20
5. Question
दी हुई आकृति में ∠ ABC और ∠ DEF दो कोण इस प्रकर से है कि BA ⊥ ED और EF ⊥ BC, तो ∠ ABC + ∠ DEF का मान ज्ञात करें।
Hint
Since the sum of all the angle of a quadrilateral is 360°
We have ∠ ABC + ∠ BQE + ∠ DEF + ∠ EPB = 360°
∴ ∠ ABC + ∠ DEF = 180°
[since BPE = EQB = 90° ]
- Question 6 of 20
6. Question
नीचे दी गई आकृति में E, AB का मध्य-बिन्दु है और F, AD का मध्य-बिन्दु है। यदि FAEC का क्षेत्रफल 13 है तो ABCD का क्षेत्रफल क्या होगा?
Hint
As F is the mid-point of AD, CF is the median of the triangle ACD to the side AD.
Hence area of the triangle FCD = area of the triangle ACF.
Similarly area of triangle BCE = area of triangle ACE.
∴ Area of ABCD = Area of (CDF + CFA + ACE + BCE)
= 2 Area (CFA + ACE) = 2 × 13 = 26 sq. units.
- Question 7 of 20
7. Question
दिया हुआ है कि AB और CD समांतर है यदि रेखा ℓ, m और n को बिन्दु O पर प्रतिच्छेद करती है, तो θ और ∠ODS का अनुपात ज्ञात करें।
Hint
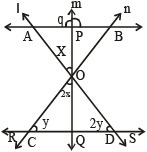
Let the line m cut AB and CD at point P and Q respectively
∠ DOQ = x (exterior angle)
Hence, Y + 2x (corresponding angle)
∴ y = x …(1)
Also . ∠ DOQ = x (vertically opposite angles)
In ∆ OCD, sum of the angles = 180⁰
∴ y + 2y + 2x + x =180°
⇒ 3x + 3y = 180°
⇒ x + y = 60 …(2)
From (1) and (2)
x = y = 30 = 2y = 60
∴ ∠ ODS = 180 – 60 = 120°
∴ θ = 180 – 3x = 180 – 3(30) = 180 – 90 = 90°.
∴ The required ratio = 90 : 120 = 3 : 4.
- Question 8 of 20
8. Question
निम्न आकृति में AB ⊥ BC और BD ⊥ AC है। CE, कोण C को प्रतिच्छेद करती है। ∠A = 30°, तो ∠CED ज्ञात करें।
Hint
In ∆ ABC, = ∠C = 180 – 90 – 30 = 60°
Again in ∆ DEC, = ∠ CED = 180 – 90 – 30 = 60°
- Question 9 of 20
9. Question
त्रिभुज ABC में कोण B एक समकोण है। यदि AC = 6 सेमी और भुजा AC पर D मध्य-बिन्दु है, तो BD की लंबाई हैः
Hint
In a right angled ∆, the length of the median is ½ the length of the hypotenuse .
Hence BD = ½ AC = 3 cm
- Question 10 of 20
10. Question
ABCD एक वर्ग है जिसका क्षेत्रफल 4 है और जो दर्शाये गए आकृति के अनुसार चार (non overlapping) त्रिभुजों में विभाजित है तो त्रिभुजों के परिमितियों का योग हैः
Hint
ABCD is square a² = 4 ⇒ a = 2
perimeters of four triangles
= AB + BC + CD + DA + 2(AC + BD)
- Question 11 of 20
11. Question
किसी चतुर्भुज की भुजाओं को नीचे दर्शाए अनुसार बढ़ाया गया हैः
x का मान क्या होगा?Hint
Sum of all the interior angles of a polygon taken in order is 360°.
i.e., x + 90 + 115 + 75 = 360
⇒ x = 360° – 280° = 80°
⇒ x = 80°
- Question 12 of 20
12. Question
किसी आयताकार क्षेत्र के दो आसन्न भुजाओं की अपेक्षा एक लड़का उस क्षेत्र के विकर्ण से होकर जाता है जिससे वह बड़ी भुजा की आधी दूरी कम चलता है। छोटी भुजा और बड़ी भुजा का अनुपात हैः
Hint
According to question,
- Question 13 of 20
13. Question
यदि दो समांतर रेखाओं को दो अलग-अलग तिर्यक छेदी रेखा प्रतिच्छेद करती है तो इन चार रेखाओं द्वारा बना चतुर्भुज होगाः
Hint
The quadrilateral obtained will always be a trapeziam as it has two lines which are always parallel to each other.
- Question 14 of 20
14. Question
निम्नलिखित आकृति में ∠ADC ज्ञात करें।
Hint
∠ACB = ∠BAC (Angles opposite equal sides are equal)
Similarly, ∠ADC = ∠CAD
∴ ∠ACB = ∠BAC
⇒ ∠ADC = ∠CAD
- Question 15 of 20
15. Question
एक त्रिभुज ABC में कोण A का आंतरिक समद्विभाजक BC से बिन्दु D पर मिलता है। यदि AB = 4, AC = 3 और ∠A = 60°, है, तो AD की लंबाई हैः
Hint
Using the theorem of angle of bisector,
In ∆ABD, by sine rule,
…(1)In ∆ABC, by sine rule;
⇒
[putting the value of sin B from (1)]
- Question 16 of 20
16. Question
दी हुई आकृति में AG = 9, AB = 12, AH = 6 है तो HC ज्ञात करें।
Hint
m ∠ AHG = 180 – 108 = 72⁰
∴ ∠ AHG = ∠ ABC …..(same angle with different names)
∴ ∆ AHG – ∆ABC …..(AA test for similarity)
AH/AB = AG/AG;
⇒ 6/12 = 9/AC
∴ AC =
= 18∴ HC = AC – AH = 18 – 6 = 12
- Question 17 of 20
17. Question
निम्न ∆ABC में, ∆ABC, DE || BC और AD/DB = 3/5 है। यदि AC = 5.6 सेमी है, तो AE ज्ञात करें।
Hint
In ∆ABC, DE || BC
By applying basic Proportionality theorem,
But
∴
⇒
⇒
⇒
⇒ 8AE = 3 × 5.6
⇒ AE = 3 × 5.6/8
∴ AE = 2.1 cm.
- Question 18 of 20
18. Question
नीचे दी गई आकृति में AB || QR है, तो PB की लंबाई ज्ञात करें।
Hint
∆PAB ~ ∆PQR
∴ PB = 2cm
- Question 19 of 20
19. Question
किसी त्रिभुज ABC में भुजाएं AB, AC और BC की लंबाईयाँ क्रमशः 3, 5 और 6 सेमी है। यदि BC पर एक बिन्दु D इस तरह से है कि रेखा AD, कोण A को आंतरिक रूप से प्रतिच्छेद करती है, तो BD की लंबाई क्या होगी?
Hint
As AD bisects ∠BAC, we have
⇒
⇒
⇒
⇒
⇒
= 2.25 cm
- Question 20 of 20
20. Question
दो अप्रतिच्छेदी वृत्तों से खींची गई स्पर्श रेखाओं की संख्या होगीः
Hint
Four tangents can be drawn to two non-intersecting circles in the following manner :
