दी हुई आकृति में, AB वृत्त की जीवा है, O वृत्त का केन्द्र है, और BT वृत्त पर स्पर्श-रेखा है. x और y का मान होगा:
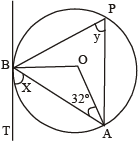
Given AB is a circle and BT is a tangent,
∠BAO = 32°
Here, ∠ OBT = 90°
[Since tangent is ⊥ to the radius at the point of contact]
OA = OB [ Radii of the same circle ]
∴ ∠ OBA = ∠OAB = 32° [ Angles opposite to equal side are equal]
∴ ∠ OBT = ∠ OBA + ∠ ABT = 90°
⇒ 32° + x = 90°.
⇒ ∠ x = 90° – 32° = 58° .
Also, ∠ AOB = 180° – ∠OAB – ∠OBA
= 180° – 32° – 32° = 116°
Now Y = ½ AOB [ Angle formed at the center of a circle is double the angle formed in the remaining part of the circle] = ½ × 116° = 58° .