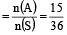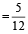Time limit: 0
Finish Test
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
- अति महत्वपूर्ण बहु वैकल्पिक प्रश्न
- ऑनलाइन प्रायिकता एक्सरसाइज, उत्तर और हल के साथ
- सभी प्रत्योगिता परीक्षाओं के लिए उपयोगी
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
- Question 1 of 20
1. Question
पाँच घोड़ों की रेस में A यादृच्छिक रूप से 2 घोड़ों पर दाँव लगाता है। इस स्थिति में उसके जीतने की प्रायिकता होगीः
Hint
- Question 2 of 20
2. Question
A के सत्य बोलने की प्रायिकता ⅘ है, जबकि B की ¾ है। एक ही तथ्य के बारे में यदि उनसे पूछा जाए तो उनके परस्पर विरोधी होने की प्रायिकता होगीः
Hint
A and B will contradict each other if one speaks truth and other false . So, the required
Probability
- Question 3 of 20
3. Question
किसी छात्र के तैराक न होने की प्रायिकता ⅕ है तो 5 छात्रों में से 4 छात्रों के तैराक होने की प्रायिकता होगीः
Hint
4 students out of 5 can be selected in ⁵C₄ ways.
Probability of a student being not a swimmer ⅕
Probability of a student being a swimmer
Required probability
- Question 4 of 20
4. Question
मैं 7 अंक बाले टेलीफोन नम्बर का अंतिम अंक भूल गया हूँ। यदि मैं प्रथम 4 सही अंक डायल करने के पश्चात् अन्तिम 3 अंक यादृच्छिक रूप से डायल करता हूँ तो सही नम्बर के डायल होने की प्रायिकता होगी:
Hint
It is given that last 3 digits are randomly dialled. Then each of the digits can be selected out of 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in 10 ways.
Hence the required probability
- Question 5 of 20
5. Question
यदि शतरंज बोर्ड के किन्हीं में दो वर्गों को यादृच्छिक रूप से चुना जाए तो उनमें से एक भुजा के उभयनिष्ट होने की प्रायिकता होगीः
Hint
Two squares out of 64 can be selected in
The number of ways of selecting those pairs which have a side in common
= ½ (4×2+24×3+36×4) = 112
[Since each of the corner squares has two neighbours each of 24 squares in border rows, other than corner ones has three neighbours and each of the remaining 36 squares have four neighbours and in this computation, each pair of squares has been considered twice].
Hence required probability
=
- Question 6 of 20
6. Question
एक पासे को इस तरह फेंका जाता है कि संख्या i आने की प्रायिकता उसके व्युत्क्रम का समानुपाती है। तब एक बार पासे को फेंकने में 3 आने की प्रायिकता होगीः
Hint
- Question 7 of 20
7. Question
किसी आलमारी में रखे 50 किताबों में एक शब्दकोष का 5 खण्ड यादृच्छिक रूप से रखा हुआ है। अगर शब्दकोष के खण्ड जरूरी नहीं है कि साथ-साथ रखे हुए हैं, तो बांये से दायें बढ़ते हुए क्रम में होने की प्रायिकता होगीः
Hint
The number of ways of arranging 50 books
= ⁵⁰P₅₀ = 50!.
The number of ways of choosing places for the five volume dictionary
= ⁵⁰C₅
and the number of ways of arranging the remaining 45 books
= ⁴⁵C₄₅= (45)!
Thus the number of favourable ways
= (⁵⁰C₅) (45 !).
Hence the probability of the required event
- Question 8 of 20
8. Question
अतुल 6 बार में से 3 बार सही निशाना लगाने में सफल होता है। भोला 6 बार में से 2 बार और चन्द्रा 4 बार में 4 बार सही निशाना लगाता है। इस बात की क्या प्रायिकता होगी कि कम से कम 2 बार में सही निशाने पर लगे (1 बार निशाना उनमें से किसी एक के द्वारा लगाना है)
Hint
Chandra hits the target 4 times in 4 shots. Hence, he hits the target definitely.
The required probability, therefore, is given by.
P(both Atul and Bhola hit) + P(Atul hits, Bhola does not hit) + P(Atul does not hit, Bhola hits)
=
- Question 9 of 20
9. Question
बैग में 5 सफेद, 7 लाल, और 8 काली गेंद हैं। यदि 4 गेंद एक के बाद एक विस्थापित करते हुए निकाली जाए तो सभी गेंदो के सफेद होने की प्रायिकता होगीः
Hint
Total number of balls
= 5 + 7 + 8 = 20
Probability that the first ball drawn is white
If balls are drawn with replacement, all the four events will have equal probability.
Therefore, required probability
- Question 10 of 20
10. Question
किसी पासे को 6 बार फेंका जाता है। यदि विषम संख्या आती है तो फेंकना ‘सफल’ माना जाता है। इस परिस्थिति में 5 बार सफल होने की प्रायिकता होगीः
Hint
Let A be the event of getting an odd number.
Here, n (S) = 6 and
n (A) = 3
Probability of getting an odd number
Hence, probability of not getting an odd number
Required probability of 5 successes
- Question 11 of 20
11. Question
6 धनात्मक और 8 ऋणात्मक संख्याएँ हैं। यादृच्छिक रूप से 4 संख्याओं को चुन कर आपस में गुणा किया जाता है। गुणनफल धनात्मक होने की प्रायिकता होगीः
Hint
Total no. of numbers
= 6 positive + 8 negative = 14
n(S) = ¹⁴C₄
The product of four numbers could be positive when,
(a) all the four numbers chosen are positive or
(b) all the four numbers chosen are negative or
(c) two of the chosen numbers are positive and two are negative.
Required Prob.
=
=
- Question 12 of 20
12. Question
दो पासे फेंकने पर उनके स्कोर का योग रूढ़ संख्या होने की प्रायिकता होगीः
Hint
Total no. of outcomes when two dice are thrown = n (S) = 36 and the possible cases for the event that the sum of numbers on two dice is a prime number, are
(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 1), (5, 6), (6, 1), (6, 5)
Number of outcomes favouring the event
= n (A) = 15
Required probability
- Question 13 of 20
13. Question
रमेश के वार्डरॉब में 3 पैंट हैं। एक काली, दूसरी नीली और तीसरी ब्राउन। उसी वार्डरॉब में 4 शर्ट भी है जिनमें से 1 काली और 3 सफेद हैं, यदि वह अंधेरे में बिना रंग देखे एक शर्ट-पैंट निकालता है तो शर्ट और पैंट के काली न होने की प्रायिकता होगीः
Hint
Probability that the trouser is not black = ⅔
Probability that the shirt is not black = ¾
Since, picking of a shirt and a trouser are independent,
required probability
- Question 14 of 20
14. Question
एक व्यक्ति 25 कारों की कतार में एक कार को न ही प्रारम्भ न ही अन्त में पार्क करता है। वापस लौटने पर उसे पता चलता है कि ठीक 15 गाड़ियां उस समय तक कतार में थी। उस व्यक्ति के कार के अगल-बगल की पार्किंग जगह के खाली होने की प्रायिकता होगीः
Hint
Exhaustive number of cases = ²⁴C₁₄
Favourable cases = ²²C₁₄
- Question 15 of 20
15. Question
यदि SOCIETY में प्रयुक्त अक्षरों को यादृच्छिक (randomly) रूप से रखा जाए तब एक साथ तीन स्वरों के आने की प्रायिकता होगीः
Hint
The word ‘society’ contains seven distinct letters and they can be arranged at random in a row in
⁷P₇ ways, i.e. in 7! = 5040 ways.
Let us now consider those arrangements in which all the three vowels come together. So in this case we have to arrange four letters. S,C,T,Y and a pack of three vowels in a row which can be done in
⁵ P₅ i.e. 5! = 120 ways.
Also, the three vowels in their pack can be arranged in
³P₃ i.e. 3! = 6 ways.
Hence, the number of arrangements in which the three vowels come together is
120 × 6 = 720
∴ The probability that the vowels come together
=
- Question 16 of 20
16. Question
यादृच्छिक रूप से चयनित किसी माह के 13 तारीख को शुक्रवार होने की प्रायिकता होगीः
Hint
Probability of selecting a month = ¹⁄₁₂.
13th day of the month is Friday if its first day is Sunday and the probability of this = ¹⁄₇.
∴ Required probability
=
. - Question 17 of 20
17. Question
यदि किसी लीप इयर का यादृच्छिक चयन किया जाए तो उस वर्ष में 53 रविवार होने की प्रायिकता होगीः
Hint
A leap-year has 366 days i.e. 52 complete weeks and two days more these two days be two consecutive days of a week. A leap year will have 53 Sundays if out of the two consecutive days of a week selected at random one is a Sunday.
Let S be the sample space and E be the event that out of the two consecutive days of a week one is Sunday, then
S = {(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
∴ n (S) = 7 and E = {(Sunday, Monday), (Saturday, Sunday)
∴ n (E) = 2
Now, required Probability, P(E) =
= ²⁄₇ - Question 18 of 20
18. Question
A और B, प्रत्येक साथ-साथ एक सिक्के को 50 बार उछालते हैं। समान उछाल (toss) में दोनों सिक्कों के टेल न आने की प्रायिकता होगी:
Hint
For each toss there are four choices
(i) A gets head, B gets head
(ii) A gets tail, B gets head
(iii) A gets head, B gets tail
(iv) A gets tail, B gets tail
thus, exhaustive number of ways
= 4⁵⁰.
Out of the four choices listed above (iv) is not favourable to the required event in a toss.
Therefore favourable number of cases is 3⁵⁰.
Hence, the required probability =
- Question 19 of 20
19. Question
मान लीजिए 6 सिक्के एक साथ उछाले जाए तो कम से कम एक टेल आने की प्रायिकता होगीः
Hint
If six coins are tossed, then the total no. of outcomes
= (2)⁶ = 64
Now, probability of getting no tail = ¹⁄₆₄
Probability of getting at least one tail
- Question 20 of 20
20. Question
किसी सिक्के को 5 बार उछाला जाता है। विषम संख्या में हेड आने की प्रायिकता होगीः
Hint
Probability of occurrence of head in a toss of a coin is 1/2.
Required probability = Prob. [Head appears once] + Prob.[Head appears thrice] + Prob. [Head appears five times]
=
=
[5 + 10 + 1]=
