Finish Test
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
- अति महत्वपूर्ण बहु वैकल्पिक प्रश्न
- ऑनलाइन नल और टंकी एक्सरसाइज, उत्तर और हल के साथ
- सभी प्रत्योगिता परीक्षाओं के लिए उपयोगी
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
- Question 1 of 20
1. Question
दो नल किसी टंकी को क्रमशः 12 और 18 मिनट में भर सकता है। दोनों नल 2 मिनट के लिए खोल दिए जाते हैं और फिर पहले नल को बंद कर दिया गया। अब टंकी को भरने में और कितने मिनट लगेंगे?
Hint
Part filled by first tap in 1 min
Part filled by second tap in 1 min
Now,
since
part of tank is filled by second tap in 1min.∴
part of tank is filled by second tap in 1 min.
= 13 min. - Question 2 of 20
2. Question
दो पाइप A और B किसी टंकी को क्रमशः 10 मिनट और 15 मिनट में भर सकता है। दोनों पाइप को एक साथ खोल दिया गया लेकिन 3 मिनट के बाद पाइप B को बंद कर दिया गया। टंकी को भरने में कितना समय लगेगा?
Hint
In one min, (A + B) fill the cistern
In 3 min, (A + B) fill the cistern
=
Remaining part
since
part filled by A in one min.∴ ½nd part filled by A in 10 × ½ = 5 minutes
∴ Total time = 3 + 5 = 8 min.
- Question 3 of 20
3. Question
दो पाइप A और B किसी टंकी को क्रमशः 12 मिनट और 16 मिनट में भर सकता है। दोनों पाइप को एक साथ खोल दिया गया लेकिन टंकी भरने से 4 मिनट पहले पाइप A को बंद कर दिया गया। टंकी को भरने में कितना समय लगेगा?
Hint
Let cistern will be full in x min. Then,
part filled by B in x min + part filled by A in
(x – 4) min = 1
- Question 4 of 20
4. Question
दो नल A और B किसी टंकी को अलग-अलग क्रमशः 40 मिनट और 45 मिनट मेें भर सकता है। वे दोनों नल, टंकी को एक साथ भरना प्रारम्भ करते हैं लेकिन कुछ मिनट बाद नल A को बंद कर दिया गया और नल B टंकी के शेष भाग को भरने में 23 मिनट के समय लिया। कितने मिनट के बाद नल A को बंद किया गया था?
Hint
Let A was turned off after x min. Then,
cistern filled by A in x min + cistern filled by B in
(x + 23) min = 1
- Question 5 of 20
5. Question
तीन पाइप A, B और C किसी टंकी को अलग-अलग क्रमशः 3, 4 और 6 मिनट में भर सकता है। पाइप A को पहले खोला गया, 1 मिनट के बाद पाइप B को खोला गया और A के खोलने के 2 मिनट बाद C को भी खोल दिया गया। टंकी को पूरी तरह से भरने में लगा समय ज्ञात करें?
Hint
Let cistern will be full in x min. Then,
part filled by A in x min + part filled by B in
(x – 1) min + part filled by c in (x – 2)min = 1
- Question 6 of 20
6. Question
तीन नल A, B और C किसी टंकी को क्रमशः 12, 15 और 20 घंटे में भर सकता है। यदि नल A पूरे समय के लिए खुला हो और नल B और C में से प्रत्येक को बारी-बारी से 1 घंटे के लिए खोला गया हो, तो टंकी को भरने में लगा समय होगाः
Hint
(A + B)’s 1 hour’s work
=
(A + C)’s 1 hour’s work
=
Part filled in 2 hrs
=
Part filled in 6 hrs
=
Remaining part
=
Now, it is the turn of A and B and 3/20 part is filled by A and B in 1 hour.
∴ Total time taken to fill the tank
= (6 + 1) hrs = 7 hrs.
- Question 7 of 20
7. Question
एक गर्म पाइप किसी टंकी को भरने मे एक ठंडे पाइप की अपेक्षा 3 मिनट अधिक समय लेता है। दोनों पाइप एक साथ मिलकर टंकी को 6 मिनट 40 सेकण्ड में भरते हैं। अकेले ठंडे पाइप द्वारा टंकी को भरने में लगा समय हैः
Hint
Let cold pipe take X minutes, then hot pipe will take (X + 3) minutes.
Together
=
40X + 60 = 3X (X + 3)
⇒ 40X + 60 = 3X² + 9X
⇒ 3X² – 31X – 60 = 0
⇒ X = 12 minutes
- Question 8 of 20
8. Question
दो पाइप P और Q किसी टंकी को क्रमशः 24 घंटे और 32 घंटे में भरता है। यदि दोनों पाइप एक साथ खोल दिये जाएँ तो बताएँ कि पहले पाइप को कब बंद करना चाहिए जिससे टंकी ठीक 16 घंटे में भर सके?
Hint
Suppose the first pipe was closed after x hrs.
Then, first’s x hrs supply + second’s 16 hrs supply = 1
or,
=1∴
= 1 – ½= ½∴ x = 12 hrs.
Quicker method :
The first pipe should work for
× 24 hrs.= 12hrs
- Question 9 of 20
9. Question
यदि दो पाइप साथ-साथ कार्य करें तो एक जलाशय 12 घंटे में भर जाता है। पहला पाइप जलाशय को दूसरे पाइप की अपेक्षा 10 घंटे अधिक तेजी से भरता है। तेजी से भरने वाले पाइप से जलाशय को भरने में कितने घंटे लगेंगे?
Hint
Let the faster pipe fills the tank in x hrs.
Then the slower pipe fills the tank in x + 10 hrs.
When both of then are opened, the reservoir will be filled in
= 12⇒ x² – 14x – 120 = 0
∴ x = 20, – 6
But x can’t be – ve, hence the faster pipe will fill the reservoir in 20 hrs.
- Question 10 of 20
10. Question
किसी टंकी में दो भरने वाला नल (जो टंकी को क्रमशः 12 मिनट और 15 मिनट में भरता है) और एक खाली करने वाला नल है। जब तीनों नलों को एक साथ खोल दिया जाता है, तो खाली टंकी को भरने में 20 मिनट लगता है। टंकी को खाली करने में खाली करने वाला नल कितना समय लेगा?
Hint
Let the exhaust tap empties the tank in x minutes.
Then,
⇒
⇒
⇒ x = 10 min
- Question 11 of 20
11. Question
एक नल किसी टंकी को 2 घंटे में भर सकता है तथा दूसरा नल टंकी को 3 घंटे में खाली कर सकता है। यदि दोनों नल एक साथ खोल दियें जाएं तो टंकी को भरने में कितना समय लगेगा?
Hint
Work of both tap for 1 hour
=
Hence, both tap will fill the cistern in 6 hours.
- Question 12 of 20
12. Question
दो पाइप किसी टंकी को क्रमशः 20 और 24 घंटे में भर सकता है और एक तीसरा पाइप 3 गैलन प्रति मिनट की दर से खाली कर सकता है। तीनों पाइप एक साथ मिलकर टंकी को 15 मिनट में भर सकता है। टंकी की क्षमता हैः
Hint
Work done by the waste pipe in 1 minute
=
[–ve sign means emptying]∴ Volume of ¹⁄₄₀ part
= 3 gallons.
Volume of whole
= (3 × 40) gallons
= 120 gallons.
- Question 13 of 20
13. Question
नल A किसी पानी टंकी को 25 मिनट में भर सकता है, नल B उसी टंकी को 40 मिनट में भर सकता है और नल C उस टंकी को 30 मिनट में खाली कर सकता है। यदि तीनों नल एक साथ खोल दिये जाएं तो कितने मिनट में टंकी पूरी तरह से भरेगी या खाली होगी?
Hint
Tank filled in 1 minute
=
part
part∴ tank will be filled complete in minutes
- Question 14 of 20
14. Question
एक पानी की टंकी का ⅖ भाग भरा हुआ है। पाइप A टंकी को 10 मिनट में भर सकता है और पाइप B इसे 6 मिनट में खाली कर सकता है। यदि दोनों पाइप एक साथ खोल दिये जाएं तो टंकी को पूरी तरह से भरने या खाली होने में कितना समय लगेगा?
Hint
Since pipe A in 1 minute fills ¹⁄₁₀ part and Pipe B in 1 min. empties ⅙ part
∴ Pipe A + B in 1 min
=
Since ¹⁄₁₅ part gets emptied in 1 min
∴ ⅖ part is emptied in
15 × ⅖ min = 6 min
- Question 15 of 20
15. Question
एक नल किसी टंकी को 16 मिनट में भर सकता है तथा दूसरा नल उसी टंकी को 8 मिनट में खाली कर सकता है। यदि टंकी का 1/2 भाग भरा हुआ है और दोनों नलों को एक साथ खोल दिया जाता है तो टंकी भरेगी या खाली होगी? इसे खाली या भरने में कितना समय लगेगा?
Hint
If both the pumps are opened together, then the tank will be emptied because the working efficiency of pump emptying is more than that of the pump filling it. Thus in 1 min net work done
=
partsor the tank will be emptied in 16 min
⇒ ½ tank will be emptied in 8 min.
- Question 16 of 20
16. Question
एक पाइप किसी टंकी को 15 मिनट में भर सकता है तथा दूसरा पाइप उसी टंकी को 10 मिनट में भर सकता है। एक तीसरा पाइप टंकी को 5 मिनट में खाली कर सकता है। प्रारम्भ में पहले दो पाइपों को 4 मिनट के लिए खोला जाता है तदुपरांत तीसरे पाइप को भी खोला जाता है। टंकी को खाली होने में कितना समय लगेगा?
Hint
Proportion of the volume of the tank filled by both the pipes in 4 min
=
= ⅔rd of the tank.
Volume of the tank filled by all the pipes working together
=
i.e. 1/30 tank is emptied in 1 min.
- Question 17 of 20
17. Question
किसी टंकी को पाइप A और B क्रमशः 5 घंटे और 6 घंटे में भर सकता है। पाइप C इस टंकी को 12 घंटे में खाली कर सकता है। यदि तीनों पाइप एक साथ खोल दिये जाएँ तो टंकी कितनी देर में भरेगी?
Hint
Net part filled in 1 hour
=
.∴ The tank will be full in
hrsi.e.,
hrs. - Question 18 of 20
18. Question
तीन पाइप A, B, और C किसी टंकी से जुड़ा हुआ है। A और B टंकी को क्रमशः 20 और 30 मिनट में भर सकता है, जबकि C इसे 15 मिनट में खाली कर सकता है। यदि A, B और C में से प्रत्येक को एक-एक करके 1 मिनट के लिए खोला जाता है तो टंकी कितनी देर में भरेगी?
Hint
1 minute’s work of each of the three pipes
i.e., work of 3 pipes for 3 minutes
=
∴ Work of 3 pipes for 55 minutes each
=
∴ Remaining part to be filled
Now, pipe A will fill 1/20 of the cistern in next 1 minute.
∴ Remaining portion to be filled by pipe B
=
– 
=
∴ Time taken by pipe B to fill 1/30 of the cistern = 1/30 × 30 = 1min
Hence, total time
= (55 × 3) + 1 + 1
= 167 min.
- Question 19 of 20
19. Question
एक पानी की टंकी में 6 पाइपों को फिट किया गया है। इसमें से कुछ भरने वाला पाइप है और अन्य टंकी खाली करने वाला पाइप है। प्रत्येक भरने वाला पाइप टंकी को 9 घंटे में भर सकता है और प्रत्येक खाली करने वाला पाइप टंकी को 6 घंटे में खाली कर सकता है। सभी पाइपों को खोल देने पर खाली टंकी 9 घंटे में भर जाती है। टंकी भरने वाले पाइप की संख्या है?
Hint
Total number of pipes = 6 (given)
Let number of inlet pipes = x
∴ number of outlet pipes = 6 –x
Now, Inlet pipe fill the tank in 9 hours and outlet pipe empty it in 6 hours.
∴ Total part filled in 1 hour
=
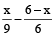
When all the pipes are opened.
But given total part filled in 9 hr
∴
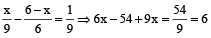
⇒ 15x = 60 ⇒ x = 4
Hence, number of inlet pipes = 4.
- Question 20 of 20
20. Question
दो पाइप A और B किसी टंकी को क्रमशः 15 घंटे और 20 घंटे में भर सकता है जबकि एक तीसरा पाइप C भरी हुई टंकी को 25 घंटे में खाली कर सकता है। प्रारंभ में सभी तीनों पाइपों को खोल दिया गया। 10 घंटे बाद C को बंद कर दिया गया। टंकी को भरने में कितना समय लगेगा?
Hint
Part filled in 10 hours
=
Remaining part
=
(A + B)’s 1 hour’s work
=
⇒
∴ The tank will be full in (10 + 2) hrs = 12 hrs.