नल और टंकी में उपयोग में आने वाले नियम, समय और कार्य के नियम की तरह ही होते है। यहाँ टंकी को भरने के लिए एक पाइप को टंकी से जोड़ा जाता है, इसे भरने वाली पाइप कहा जाता है और टंकी को खाली करने के लिए जिस पाइप को जोड़ा जाता है उसे निकासी पाइप कहा जाता है।
प्रश्नों को हल करने की संक्षिप्त विधि
यदि कोई पाइप किसी टंकी को A घंटे में भरता हो तो 1 घंटे में भरा गया हिस्सा = 1/A
यदि पाइप-A, पाइप-B से X गुना बड़ा हो तब पाइप-A, पाइप-B की अपेक्षा, टंकी को भरने में 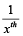 समय लेगा।
समय लेगा।
उदाहरण 1. यदि पाइप-A, 100 लीटर की टंकी को भरने में 4 घंटे का समय लेता है तो पाइप-B जो कि दोगुने आकार का है, उस टंकी कोे कितने समय में खाली करेगा?
हल: चूँकि पाइप-B दोगुने आकार का है, इसलिए यह पाइप-A की अपेक्षा आधे समय में टंकी को खाली करेगा।
इस प्रकार 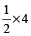 = 2 घंटे
= 2 घंटे
यदि कोई पाइप किसी टंकी को a घंटे में भरता हो और एक दूसरी पाइप टंकी को b घंटे में खाली करता हो, तो 1 घंटे में भरा गया (या खाली) हिस्सा, जब दोनों पाइप खुली हो
= 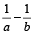
1 घंटे में भरने या खाली करने के लिए आवश्यक समय
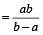
यदि नल X और Y एक टंकी को क्रमशः m और n घंटे में खाली/भरता हो तो दोनों नलों को एक साथ खोल देने पर खाली टंकी को भरने में लगा समय = 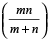 घंटे
घंटे
यदि नल X किसी टंकी को m घंटों में भरता है तथा दूसरा निकासी नल Y इस टंकी को n घंटों में खाली करता है तो दोनों नलों को एक साथ खोल देने पर, खाली टंकी को भरने या खाली करने में लगा समय = 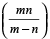 घंटे
घंटे
उदाहरण 2. 1000 लीटर वाली किसी टंकी को भरने वाला नल 2 घंटे में भर सकता है तथा दूसरा निकासी नल इस टंकी को 4 घंटे में खाली कर सकता है। यदि दोनों नलों को एक साथ खोल दिया जाए तो टंकी को भरने में कितना समय लगेगा? एक घंटे में टंकी का कितना हिस्सा भरेगा?
हल: टंकी को भरने में लिया गया समय = 2 घंटे
टंकी को खाली करने में लिया गया समय = 4 घंटे
टंकी को भरने में लिया गया समय
= 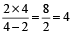 घंटे
घंटे
1 घंटे में भरा गया कुल हिस्सा
= टंकी का 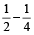 भाग
भाग
= टंकी का 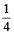 भाग
भाग
यदि एक पाइप किसी टंकी को a मिनट में भर सकता है, किन्तु टंकी में लीकेज होने के कारण इस टंकी के भरने में X मिनट ज्यादा समय लगता हो तो भरी हुई टंकी के खाली होने में लगा समय
= 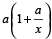
उदाहरण 3. 1000 लीटर वाली टंकी को कोई नल 2 घंटे में भर सकता है किन्तु इसमें एक छेद होने के कारण इस टंकी को भरने में 2 घंटे अधिक समय लगता है। यह छेद इस भरी हुई टंकी को कितने समय में खाली करेगा?
हल: टंकी को भरने में लिया गया समय = 2 घंटे
छेद के कारण लिया गया अतिरिक्त समय = 2 घंटे
छेद के कारण टंकी को खाली होने में लगा समय
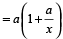

= 2 × 2 = 4 घंटे
यदि एक पाइप किसी टंकी को x घंटे में भरता है और एक अन्य पाइप उसी टंकी को y घंटे में भरता है लेकिन एक तीसरी पाइप पूरी टंकी को z घंटे में खाली करता है, जबकि सभी को एक साथ खोल दिया जाता है तो 1 घंटे में भरा हुआ कुल हिस्सा 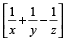
टंकी को भरने में लिया गया समय
= 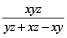 घंटे
घंटे
एक टंकी में एक छेद होने के कारण x घंटे में खाली हो जाती है। एक पाइप जो प्रति घंटे y लीटर पानी भरता है, को भी एक साथ खोल दिया जाता है तो वह टंकी z घंटे में खाली हो जाती है, तब टंकी की क्षमता 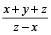 लीटर होगी।
लीटर होगी।
एक टंकी को तीन पाइपों जिसका व्यास क्रमशः x सेमी, y सेमी और z सेमी (जहाँ x < y < z) द्वारा भरा गया। तीनों पाइपों को एक साथ खोल दिया जाता है। यदि सबसे बड़ी पाइप टंकी को P मिनट में भरता हो और प्रत्येक पाइप से बहने वाले पानी की मात्रा, इसके व्यास के वर्ग के समानुपाती हो, तो तीनों पाइपों द्वारा टंकी को भरने में लिया गया समय 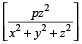 मिनट होगा।
मिनट होगा।
यदि एक भरने वाली पाइप A जो B से n गुणा तेज है, किसी टंकी को भरने में x मिनट कम समय लेता हैं। यदि दोनों पाइपों को एक साथ खोल दिया जाता है तो वे टंकी को भरने में 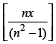 मिनट लेंगे।
मिनट लेंगे।
A टंकी को 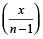 मिनट में भरेगा और B टंकी को
मिनट में भरेगा और B टंकी को 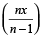 मिनट में भरेगा।
मिनट में भरेगा।
(यहाँ A ज्यादा तेजी से भरने वाला पाइप और B कम तेजी से भरने वाला पाइप है।)
दो भरने वाला पाइप A और B एक साथ किसी टंकी को t मिनट में भर सकता है। यदि पहला पाइप A अकेले t की अपेक्षा x मिनट ज्यादा या कम समय लेता हो और दूसरा पाइप B अकेले t की अपेक्षा y मिनट ज्यादा या कम समय लेता हो, तो 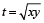 मिनट।
मिनट।
उदाहरण 4. पाइप-A किसी टंकी को 20 घंटे में भर सकता है जबकि पाइप-B अकेले टंकी को 30 घंटे में भर सकता है और पाइप-C पूरी टंकी को 40 घंटे में खाली कर सकता है। यदि सभी पाइपों को एक साथ खोल दिया जाता है तो टंकी को भरने में कितना समय लगेगा?
हल: सूत्र से, टंकी को भरने में लिया गया समय
= 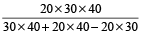
= 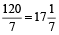 घंटे
घंटे
उदाहरण 5. तीन पाइप A, B तथा C किसी टंकी को क्रमशः 6 मिनट, 8 मिनट और 12 मिनट में भर सकता है। टंकी भरने से 6 मिनट पहले पाइप C को बंद कर दिया गया। टंकी को भरने में कितना समय लगेगा?
- 4 मिनट
- 6 मिनट
- 5 मिनट
- डाटा अपर्याप्त
हल: (1): माना टंकी को भरने में t मिनट लगता है।
अब, 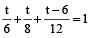
या 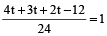
या 9t – 12 = 24
या 9t = 36
∴ t = 4 मिनट.
उदाहरण 6. चार पाइप किसी जलाशय को क्रमशः 15, 20, 30 और 60 घंटे में भर सकता है। पहले पाइप को 6 am, दूसरे पाइप को 7 am, तीसरे पाइप को 8 am और चौथे पाइप को 9 am पर खोला गया। जलाशय कब भरेगा?
हल: माना 6 am के बाद भरने में लिया गया समय t घंटा है।
∴ 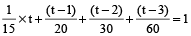
∴ 4t + 3 (t – 1) + 2 (t – 2) + (t – 3) = 60
∴ t = 7 घंटा∴ यह दोपहर 1 बजे भरेगा।
