गुणक और गुणजः यदि एक संख्या ‘x’ दूसरी संख्या ‘y’ को पूर्णतः विभाजित करती है तो हम ‘x’ को ‘y’ का गुणक कहते हैं। इस अवस्था में ‘y’, ‘x’ का गुणज कहलाता है।
गुणनखण्डः जब कोई संख्या किसी दूसरी संख्या को पूरा-पूरा विभाजित करे और शेष कुछ न बचे तो वह संख्या उस दूसरी संख्या का गुणनखण्ड कहलाती है।
जैसे- संख्या 15, 3 और 5 से पूरी-पूरी विभाजित हो जाती है। अतः 3 और 5, 15 के गुणनखण्ड होंगे।
महत्तम समापवर्तक (HCF)
दो या दो से अधिक संख्या का महत्तम समापवर्तक वह बड़ी से बड़ी संख्या होती है, जो प्रत्येक दी गई संख्याओं को पूरा-पूरा विभाजित कर सके।
महत्तम समापवर्तक हम निम्नलिखित दो विधियों द्वारा ज्ञात कर सकते हैं:
1. अभाज्य गुणनखण्ड विधि
उदाहरण: 144, 180 और 108 का महत्तम समापवर्तक इस विधि द्वारा निम्न प्रकार ज्ञात कर सकते हैं –
- 144 = 2 × 2 × 2 × 2 × 3 × 3
- 108 = 2 × 2 × 3 × 3 × 3
- 180 = 2 × 2 × 3 × 3 × 5
उपरोक्त तीनों संख्याओं के अभाज्य गुणनखण्डों में उभयनिष्ठ गुणनखण्ड
2 × 2 × 3 × 3 = 36 है।
∴ 144, 180 और 108 का अभीष्ट महत्तम समापवर्तक 36 होगा।
2. भाग विधि
उदाहरण: उपरोक्त संख्याओं का महत्तम समापवर्तक भाग विधि द्वारा निम्न प्रकार ज्ञात कर सकते हैं –
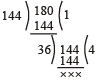
अब 36 और 108 का महत्तम समापवर्तक ज्ञात करना है।
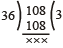
अतः 144,180 और 108 का महत्तम समापवर्तक 36 होगा।
लघुत्तम समापवर्त्य (LCM)
दो या दो से अधिक दी गई संख्याओं का लघुत्तम समापवर्त्य वह छोटी से छोटी संख्या होती है जो प्रत्येक दी गई संख्या से पूरी-पूरी विभाजित हो सके।
लघुत्तम समापवर्त्य हम निम्नलिखित दो विधियों द्वारा ज्ञात कर सकते हैं:
1. अभाज्य गुणनखण्ड विधि
उदाहरण: 12, 16 तथा 30 का लघुत्तम समापवर्त्य इस विधि द्वारा निम्न प्रकार ज्ञात कर सकते हैं-
- 12 = 2 × 2 × 3
- 16 = 2 × 2 × 2 × 2
- 30 = 2 × 3 × 5
अब तीनों संख्याओं के अभाज्य गुणनखंडों में 2 सबसे अधिक 4 बार तथा 3 एक बार और 5 एक बार आया है।
इस प्रकार दी गई संख्याओं का अभीष्ट लघुत्तम समापवर्त्य
= 2 × 2 × 2 × 2 × 3 × 5 = 240 होगा।
2. भाग विधि
उदाहरण: उपरोक्त संख्याओं का लघुत्तम समापवर्त्य भाग विधि द्वारा इस प्रकार ज्ञात करेंगे:
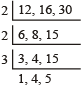
∴ दी गई संख्याओं का अभीष्ट लघुत्तम समापवर्त्य
= 2 × 2 × 3 × 1 × 4 × 5 = 240 होगा।
भिन्नों का महत्तम समापवर्तक और लघुत्तम समापवर्त्य
1. दी गई भिन्नों का महत्तम समापवर्तक

उदाहरण: 1/2 और 3/4 का महत्तम समापवर्तक

2. दी गई भिन्नों का लघुत्तम समापवर्त्य

उदाहरण: 1/2 और 3/4 का लघुत्तम समापवर्त्य

दो संख्याओं का गुणनफल = (उन संख्याओं का HCF) × (उन संख्याओं का LCM)
