चालः किसी पिण्ड द्वारा इकाई समय में तय की गई दूरी को उसकी चाल कहते हैं।
- चाल = दूरी/समय
- दूरी = चाल × समय और
- समय = दूरी/चाल
मात्रक: (Units)
- समय: सेकेण्ड, मिनट, घंटा
- दूरी: मीटर, किलोमीटर
- चाल: किमी/घंटा, मीटर/सेकेण्ड
इकाइयों का रूपांतरण:
- 1 किमी/घंटा = 5/18 मीटर/सेकेण्ड
- 1 मीटर/सेकेण्ड = 18/5 किमी/घंटा
- 1 किमी/घंटा = 5/8 मील/घंटा
- 1 मील/घंटा = 22/15 फुट/सेकेण्ड
उदाहरण 1. एक स्कूटर सवार 45 किमी/घंटा की चाल से 4 मिनट में कितनी दूरी तय कर लेगा?
हल: स्कूटर सवार की चाल = 45 किमी/घंटा
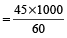 = 750 मीटर/मिनट
= 750 मीटर/मिनट
∴ 4 मिनट में तय की गई दूरी = 4 × 750 = 3000 मीटर
प्रश्नों को हल करने की संक्षिप्त विधि
औसत चाल
किसी पिण्ड द्वारा तय की गई कुल दूरी तथा उस दूरी को तय करने में लगे कुल समय के अनुपात को उस पिण्ड की औसत चाल कहते हैं।

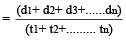
यदि कोई व्यक्ति X से Y किमी की दूरी A मीटर/सेकेण्ड की चाल से और Y से X किमी की दूरी B मीटर/सेकेण्ड की चाल से तय करें तो पूरी यात्रा के दौरान औसत चाल = 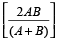 मीटर/सेकेण्ड
मीटर/सेकेण्ड
उदाहरण 2. सुनील दिल्ली से पटना की यात्रा 40 किमी/घंटा की चाल से तय करता है और वापस दिल्ली 50 किमी/घंटा की चाल से आता है। यात्रा की औसत चाल क्या है?
हल: सूत्र के अनुसार, औसत चाल
= 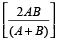 =
= 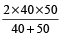 =
= 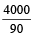
= 44.44 किमी/घंटा
किसी निश्चित दूरी ‘d’ की यात्रा में यदि एक व्यक्ति की चाल में परिवर्तन का अनुपात m:n हो, तो उसके समय में परिवर्तन का अनुपात n:m होगा।
यदि कोई पिंड A से B के बीच की ‘d’ दूरी को ‘a’ चाल से t₁ समय में तय करता है और B से A की दूरी अर्थात बराबर दूरी अपने सामान्य चाल ‘a’ का m/n चाल से वापस आता है तो उस बराबर दूरी को तय करने में लगे समय में परिवर्तन
=  × t₁; जहाँ n > m
× t₁; जहाँ n > m
=  × t₁; जहाँ m > n
× t₁; जहाँ m > n
यदि दूरी का पहला भाग t₁ समय में v₁ चाल से तय किया गया हो और दूरी का दूसरा भाग t₂ समय में v₂ चाल से तय किया गया हो, तो औसत चाल होगा
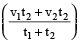
आपेक्षिक चाल (Relative Speed)
जब कोई दो गतिशील पिंड विपरीत दिशा में जा रही हो तो उसकी आपेक्षिक चाल उन दोनों पिंडों की चालों का योग होता है। इसके विपरीत यदि दोनों पिंड एक ही दिशा में जा रही हो तो उनका आपेक्षिक चाल उन दोनों पिंडों की चालों का अंतर होता है।
उदाहरण के तौर पर जब दो ट्रेनें विपरीत दिशा में क्रमशः x किमी/घंटा और y किमी/घंटा के चाल से गतिमान हो तो उनकी आपेक्षिक गति (x + y) होगी। दूसरी स्थिति में जब वही दो ट्रेने समान दिशा में गतिमान हो तो उनकी आपेक्षिक गति (x – y) होगी।
पहली स्थिति में पहली ट्रेन दूसरी ट्रेन को 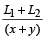 घंटे में पूरी तरह पार करेगी जबकि दूसरी स्थिति में पहली ट्रेन दूसरी ट्रेन को
घंटे में पूरी तरह पार करेगी जबकि दूसरी स्थिति में पहली ट्रेन दूसरी ट्रेन को 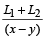 घंटे में पार करेगी जहां L₁ और L₂ ट्रेन की लम्बाईयां हैं।
घंटे में पार करेगी जहां L₁ और L₂ ट्रेन की लम्बाईयां हैं।
उदाहरण 3. 100 मीटर और 80 मीटर लंबाई वाली दो रेलगाड़ियाँ समान दिशा में गतिमान हैं। यदि पहली रेलगाड़ी 51 मीटर/सेकेण्ड की चाल से और दूसरी रेलगाड़ी 42 मीटर/सेकेण्ड की चाल से गतिमान है तो उन्हें एक-दूसरे को पार करने में कितना समय लगेगा?
हलः यहाँ, पहली रेलगाड़ी की लंबाई = 100 मीटर
दूसरी रेलगाड़ी की लंबाई = 80 मीटर
और पहली रेलगाड़ी की चाल = 51 मीटर/सेकेण्ड
दूसरी रेलगाड़ी की चाल = 42 मीटर/सेकेण्ड
चूँकि रेलगाड़ियाँ समान दिशा में हैं।
∴ आपेक्षिक चाल = 51 – 42 = 9 मीटर/सेकेण्ड
सूत्र के अनुसार अभीष्ट समय
= 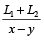
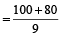 = 20 सेकेण्ड
= 20 सेकेण्ड
उदाहरण 4. 100 मीटर और 80 मीटर लंबाई वाली दो रेलगाड़ियाँ विपरीत दिशा में गतिमान हैं। यदि पहली रेलगाड़ी 10 मीटर/सेकेण्ड की चाल से और दूसरी रेलगाड़ी 15 मीटर/सेकेण्ड की चाल से गतिमान है तो उन्हें एक-दूसरे को पार करने में कितना समय लगेगा?
हल: पहली रेलगाड़ी की लंबाई = 100 मीटर
दूसरी रेलगाड़ी की लंबाई = 80 मीटर
और पहली रेलगाड़ी की चाल = 10 मीटर/सेकेण्ड
दूसरी रेलगाड़ी की चाल = 15 मीटर/सेकेण्ड
आपेक्षिक चाल = 10 + 15 = 25 मीटर/सेकेण्ड
(चूँकि रेलगाड़ियाँ विपरीत दिशा में हैं।)
सूत्र के अनुसार अभीष्ट समय
= 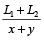
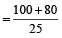 = 7.2 सेकेण्ड
= 7.2 सेकेण्ड
उदाहरण 5. एक मारूती कार ड्राइवर कार को 68 किमी/घंटा की चाल से चला रहा है। वह एक बस जो उससे 40 मीटर आगे है की ओर जा रहा है। 10 सेकेण्ड के बाद बस उससे 60 मीटर पीछे हो जाती है। बस की चाल हैः
- 30 किमी/घंटा
- 32 किमी/घंटा
- 25 किमी/घंटा
- 38 किमी/घंटा
हल: (2) माना बस की चाल = SB किमी/घंटा
अब, 10 सेकेण्ड में कार द्वारा तय की गई सापेक्षिक दूरी
= (60 + 40) मीटर = 100 मीटर
∴ कार की सापेक्षिक चाल =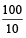
= 10 मीटर/सेकेण्ड = 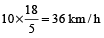
∴ 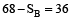
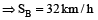
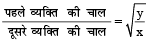
यदि दो व्यक्ति (या गाड़ी या ट्रेन) एक ही समय में दो बिन्दु A और B से एक-दूसरे के विपरीत दिशा में यात्रा करना प्रारंभ करें तो एक-दूसरे को पार करने के बाद उन्हें अपनी यात्रा पूरी करने में क्रमशः X और Y घंटे लगते हो, तब
उदाहरण 6. एक ट्रेन A से B की ओर तथा एक दूसरी ट्रेन B से A की ओर एक ही समय में जा रही है। एक-दूसरे को पार करने के बाद उन्हें अपनी यात्रा पूरी करने में क्रमशः 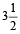 और
और 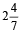 घंटे लगते हैं। यदि पहले ट्रेन की चाल 60 किमी/घंटा हो, तो दूसरी ट्रेन की चाल ज्ञात करें।
घंटे लगते हैं। यदि पहले ट्रेन की चाल 60 किमी/घंटा हो, तो दूसरी ट्रेन की चाल ज्ञात करें।
हल: 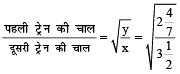
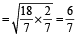
∴ 
⇒ दूसरी ट्रेेन की चाल = 70 किमी/घंटा
यदि नयी चाल सामान्य चाल का a/b हो, तो सामान्य समय 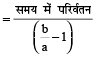
उदाहरण 7. एक लड़का अपने सामान्य चाल के 3/5 चाल से 14 मिनट देर से स्कूल पहुँचता है। उसके स्कूल पहुँचने का सामान्य समय ज्ञात करें?
हल: सामान्य समय = 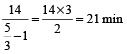
x मीटर लंबे किसी ट्रेन द्वारा एक सिग्नल को पार करने में लिया गया समय उस ट्रेन द्वारा x मीटर दूरी तय करने में लगे समय के बराबर होता है।
उदाहरण 8. एक 300 मीटर लंबे ट्रेन की चाल 10 m/s है। इसे एक इलेक्ट्रिक पोल को पार करने में कितना समय लगेगा?
हल: 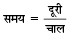
यहाँ ट्रेन की लंबाई ही दूरी होगी जो 300 मीटर है।
∴ समय = 300/10 = 30 सेकेण्ड
x मीटर लंबे ट्रेन द्वारा y मीटर लंबे किसी वस्तु को पार करने में लगा समय उस ट्रेन द्वारा (x + y) मीटर दूरी तय करने में लगे समय के बराबर होता है।
उदाहरण 9. 300 लंबे ट्रेन की चाल 10 m/s है। इसे 50 मीटर लंबे प्लेटफार्म को पार करने में कितना समय लगेगा?
हल: 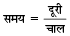
यहाँ, (ट्रेन की लंबाई + प्लेटफार्म की लंबाई) दूरी होगी।
अर्थात् 300 + 50 = 350 m दूरी होगी।
अतः समय = 350/10 = 35 सेकेण्ड
एक व्यक्ति निश्चित दूरी D तय करता है। यदि वह S₁ तेज चाल से चलता तो उस दूरी तय करने में t समय कम लगता और यदि वह S₂ धीमी चाल से चलता है तो उसे उस दूरी तय करने में t समय ज्यादा लगता तो वास्तविक चाल होगी
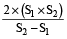
उदाहरण 10. एक व्यक्ति स्कूटर से एक निश्चित दूरी तय करता है। यदि वह 3 किमी/घंटा तेज रफ़्तार से जाता है तो उसे 20 मिनट कम समय लगता। यदि वह 2 किमी/घंटा धीमी रफ़्तार जाता है तो उसे 20 मिनट ज्यादा समय लगता है। वास्तविक चाल ज्ञात करें।
हल: चाल 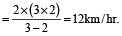
यदि एक व्यक्ति दो भिन्न चालों U और V से समान दूरी तय करता हो, तो अभीष्ट दूरी 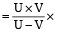 पहुचने के दोनों समयों के बीच का अंतर
पहुचने के दोनों समयों के बीच का अंतर
और अभीष्ट दूरी = दूरी तय करने में लगा कुल समय 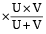
उदाहरण 11. एक लड़का 10 किमी/घंटा की चाल से चलकर अपने स्कूल 12 मिनट देर से पहुँचता है। अगली बार वह 15 किमी/घंटा की चाल से चलकर अपने स्कूल 7 मिनट देर से पहुँचता है। उसके घर से स्कूल तक की दूरी ज्ञात करें।
हल: दोनों समयों के बीच का अंतर
= 12 – 7 = 5 मिनट 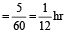
अभीष्ट दूरी = 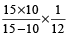
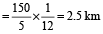
कोई व्यक्ति किसी स्थान A से t₁ समय पर चलना प्रारंभ करता है और t₂ समय पर स्थान B पर पहुँचता है। एक दूसरा व्यक्ति स्थान B से t₃ समय पर चलना प्रारंभ करता है और स्थान A पर t₄ समय पर पहुँचता है। वे दोनों आपस में मिलेंगेः
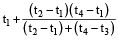
उदाहरण 12. एक बस लुधियाना से 5 बजे सुबह निकलती है और दिल्ली दोपहर 12 बजे पहुँचती है। एक दुसरी बस दिल्ली से 8 बजे सुबह निकलती है और लुधियाना शाम 3 बजे पहुँचती है। किस समय दोनों बसें एक-दूसरे से मिलेंगी?
हल: दिए हुए सभी समय को 24 hour clock time, में बदलने पर पाते हैं।
5 am = 500, 12 noon = 1200, 8 am = 800 और 3 pm = 1500
अभीष्ट समय 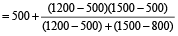
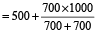 = 1000 = 10 am
= 1000 = 10 am
दो अलग-अलग साधनों से यात्रा में लिए गए समय के बीच संबंध हैः
t₂x + t₂y = 2(tx + ty)
जहाँ,
- tx = समय जो साधन X का उपयोग एक तरफ की यात्रा के लिए किया जाता है।
- ty = समय जो साधन Y का उपयोग एक तरफ की यात्रा के लिए किया जाता है।
- t₂x = समय जो साधन X का उपयोग दोनों तरफ की यात्रा के लिए किया जाता है।
- t₂y = समय जो साधन Y का उपयोग दोनों तरफ की यात्रा के लिए किया जाता है।
उदाहरण 13. एक व्यक्ति साइकिल से जाने और स्कूटर से वापस आने में 6 घंटे और 30 मिनट का समय लगाता है। यदि वह दोनों तरफ साइकिल से यात्रा करता है तो उसे 2 घंटा 10 मिनट ज्यादा लगता। दोनों तरफ स्कूटर से यात्रा करने पर उसे कितना समय लगेगा?
- 2 घंटे
- 4⅓ घंटे
- 3⅓ घंटे
- 5⅓ घंटे
हल: (2) स्कूटर द्वारा दोनों तरफ से यात्रा करने पर समय
= 6h-30m – 2h-10m = 4h-20m = 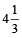 h
h
