क्षेत्रमिति के अंतर्गत हम किसी द्विविमीय या त्रिविमीय आकृतियों के क्षेत्रफल, परिमाप, आयतन आदि का अध्ययन करते हैं। इस अध्याय से संबंधित प्रश्नों को हल करने के लिए निम्नलिखित सूत्रों को जानना आवश्यक है।
द्विविमीय आकृतियाँ (Two Dimensional Figures)
आयत (Rectangle)
क्षेत्रफल = लम्बाई × चौड़ाई
परिमिति = 2 (लम्बाई + चौड़ाई)
विकर्ण =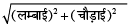 
वर्ग (Square)
क्षेत्रफल = (भुजा) ²
परिमिति = 4 × भुजा
विकर्ण =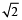 
× भुजा
त्रिभुज (Triangle)
विषमबाहु त्रिभुजः यदि a, b तथा c क्रमशः पहली, दूसरी और तीसरी भुजा की लम्बाईयाँ हो तब
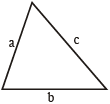
(s = अर्ध-परिमिति) =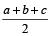 
और, क्षेत्रफल =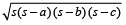 
समकोण त्रिभुज
यदि त्रिभुज समकोण हो, तब
क्षेत्रफल = 1/2 × आधार × ऊँचाई
समबाहु त्रिभुज
यदि त्रिभुज समबाहु हो, तब
क्षेत्रफल =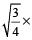 
(भुजा) ²
a भुजा वाली समबाहु त्रिभुज के अन्तः वृत्त की त्रिज्या =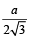 
a भुजा वाली समबाहु त्रिभुज के परिवृत्त की त्रिज्या =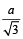 
वृत्त (Circle)
क्षेत्रफल = π × (त्रिज्या)²
परिधि = 2π × त्रिज्या
त्रिज्या = 
अर्द्ध-वृत्त (Semicircle)
अर्द्ध-वृत्त का क्षेत्रफल = 1/2 × π R²
अर्द्ध-वृत्त की परिमिति = (π R + 2R)
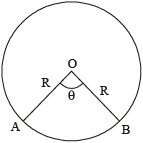
चाप की लम्बाई =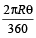 
वृत्तखण्ड AOB का क्षेत्रफल
= 1/2 × (चाप AB) × R =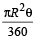 
कमरे की चार दीवारों का:
क्षेत्रफल = 2 × ऊंचाई (लम्बाई + चौड़ाई)
ऊंचाई = 
चतुर्भुज (Quadrilateral)
समांतर चतुर्भुज (Parallelogram)
क्षेत्रफल = आधार × ऊँचाई
समचतुर्भुज (Rhombus)
क्षेत्रफल = 1/2 × विकर्णों का गुणनफल
समलम्ब चतुर्भुज (Trapezium)
क्षेत्रफल = 1/2 × (समान्तर भुजाओं का योग) × उनके बीच की दूरी
विषमबाहु चतुर्भुज (Trapezoid)
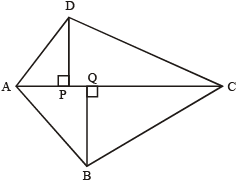
क्षेत्रफल = ½ (DP + BQ) × AC
त्रिविमीय आकृतियाँ (Three dimensional Figures)
घनाभ (Cuboid)
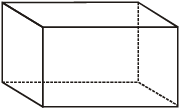
यदि घनाभ की लम्बाई, चौड़ाई तथा ऊँचाई क्रमशः L, B और H हो तब
आयतन = L × B × H
सम्पूर्ण पृष्ठ का क्षेत्रफल = 2 (L × B + B × H + H × L)
विकर्ण =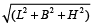 
घन (Cube)
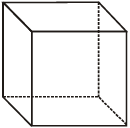
यदि घन की प्रत्येक भुजा a हो, तब
आयतन = a × a × a = a³
सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(a × a + a × a + a × a) = 6a²
घन का विकर्ण =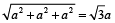 
बेलन (Cylinder)
यदि बेलन की त्रिज्या r तथा ऊँचाई या लम्बाई h हो, तब
आयतन = πr²h
क्षेत्रफल = 2πrh
सम्पूर्ण पृष्ठ का क्षेत्रफल = (2πrh + 2πr²)
शंकु (Cone)
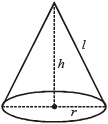
यदि शंकु के आधार की त्रिज्या, ऊँचाई तथा इसकी तिर्यक-ऊँचाई क्रमशः r, h तथा ℓ हो, तब:
आयतन =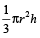 
वक्र-पृष्ठ का क्षेत्रफल = πrℓ
सम्पूर्ण पृष्ठ का क्षेत्रफल = πrℓ + πr²
तिर्यक ऊँचाई = ℓ =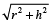 
गोला (Sphere)
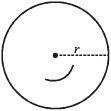
यदि गोले की त्रिज्या r हो, तब
आयतन =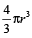 
वक्र-पृष्ठ क्षेत्रफल = 4πr²
अर्द्ध-गोला (Semisphere)
आयतन =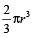 
वक्र-पृष्ठ क्षेत्रफल = 2πr²
सम्पूर्ण पृष्ठ क्षेत्रफल = 2πr² + πr² = 3πr²