किसी दी गई राशियों का औसत प्राप्त करने के लिए उन समस्त राशियों के योग में राशियों की संख्या से भाग देते हैं।
अतः औसत 
उदाहरण : संख्याएँ 3, 5 और 7 का औसत 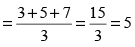 होगा।
होगा।
प्रश्नों को हल करने की विधियाँ
उदाहरण 1: किसी कक्षा के 4 विद्यार्थियों के प्राप्तांकों का औसत 65 है, तो समस्त राशियों का योग ज्ञात करें।
हल: यहाँ, राशियों की संख्या = 4
औसत = 65
∴ समस्त राशियों का योग = 65 × 4 = 260
1. समस्त राशियों का योग = औसत × राशियों की संख्या
2. दो भिन्न ज्ञात समूहों का औसत
माना समूह A, जिसमें m राशियाँ हैं का औसत a है और समूह B, जिसमें n राशियाँ का औसत b है तो समूह C, जिसमें a + b राशियाँ हैं का औसत:
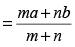 होगा।
होगा।
उदाहरण 2: एक कक्षा में 30 विद्यार्थी हैं। प्रथम 10 विद्यार्थियों का उम्र का औसत 12.5 वर्ष और अगले 20 विद्यार्थियों का उम्र का औसत 13.1 वर्ष है। पूरी कक्षा का औसत ज्ञात करें।
हल: 10 विद्यार्थियों का कुल उम्र = 12.5 × 10 = 125 वर्ष
20 विद्यार्थियों का कुल उम्र = 13.1 × 20 = 262 वर्ष
∴ 30 विद्यार्थियों का औसत उम्र
= 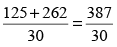 = 12.9 वर्ष
= 12.9 वर्ष
3. यदि एक समूह में एक या एक से अधिक नयी राशियों को जोड़ा या घटाया जाता है तो नयी राशि या जोड़ी या घटायी गयी राशियों का योग
= (परिवर्तित राशियों की संख्या × मूल औसत)
± (परिवर्तित औसत × अंतिम राशियों की संख्या)
यदि राशि जोड़ी जाती है तो (+) चिन्ह और यदि घटायी जाती है तो (-) चिन्ह का उपयोग करेंगे।
उदाहरण 3: एक कक्षा के 24 विद्यार्थियों के भार का औसत मान 35 किग्रा है। यदि इस मान में शिक्षक के भार को जोड़ा जाता है तो औसत भार में 400 ग्राम की वृद्धि हो जाती है। शिक्षक का भार ज्ञात करें।
हल: 24 विद्यार्थियों का कुल भार = (24 × 35) = 840 किग्रा
24 विद्यार्थियों और शिक्षक का भार = (25 × 35.4) = 885 किग्रा
∴ शिक्षक का भार = (885 – 840) = 45 किग्रा
